ESL: Ch 8. Model Inference and Averaging
Contents
8.1 Introduction
8.2 The Bootstrap and Maximum Likelihood Methods
8.3 Bayesian Methods
8.4 Relationship Between the Bootstrap and Bayesian Inference
8.5 The EM Algorithm
8.6 MCMC for Sampling from the Posterior
8.7 Bagging
8.8 Model Averaging and Stacking
8.9 Stochastic Search: Bumping
8.1 Introduction
많은 경우, 통계 모형의 학습은 sum of squares를 최소화하거나(regression), cross-entropy를 최소화(classification)하는 paramter의 값을 찾는 것으로 이루어진다. 사실 이 두 경우는 각각 maximum likelihood의 특수한 경우이다. 이 챕터에서는 Maximum likelihood를 통한 통계적 추론의 일반적인 설명을 다루고, Bayesian 통계학의 관점에서는 어떻게 통계적 추론을 하는지에 대해 다룬다. 또한 이와 같은 문맥에서, bootstrap이 maximum likelihood, Bayesian inference와 어떤 관계가 있는지 살펴본다. 또한, model averaging을 통해 모형의 성능을 개선하는 committee method, bagging, stacking, bumping에 대해서도 알아본다.
8.2 The Bootstrap and Maximum Likelihood Methods
8.3 Bayesian Methods
통계학은 크게, Frequentist(빈도론자)통계학과 Bayesian 통계학의 두 부류로 나뉜다. Frequentist 통계학과 Bayesian 통계학의 방법론적 차이는 각각 그들이 “확률”을 어떻게 이해하는가의 차이에서 기인한다.
Frequentist들은 어떤 사건의 확률을 “반복 시행할 때, 사건 발생의 상대적 빈도의 극한값(the limit of its relative frequency in a large number of trials)”으로 이해한다. 동전을 던지는 사건을 무한히 반복하면, 해당 동전의 물리적 속성에 의해 앞면이 나온 빈도(Frequency)는 0.5에 수렴할 것이고, 따라서 동전을 던져 앞면이 나오는 사건의 확률을 0.5로 정의하는 것이다. 이와 같은 관점에서는 어떤 확률변수의 확률분포 역시 무한히 반복 시행했을 때 그 분포의 극한값으로 볼 수 있고, 따라서 확률분포를 정의하는 모수(parameter)가 하나의 정해진 (그러나 많은 경우 unknown) 값, 즉 상수가 된다. Asymptotic theory, 가설 검정 등 오늘날 통계학의 근간을 이루는 상당수의 부분이 이 frequentist 관점에서 쓰여졌다.
그에 반해, Bayesian은 어떤 사건의 확률을 “그 사건에 대한 합리적인 기대, 지식 혹은 믿음의 정도”로 이해한다. 이를 모두가 공유하는 합리적인 기대의 정도로 보느냐, 개인의 주관적 지식 또는 믿음의 정도로 보느냐에 따라 객관적 Bayesian과 주관적 Bayesian의 관점으로 나눌 수 있다고 한다. 다만 여기서는 그 차이에 대해서는 언급하지 않겠다. Bayesian은 아래와 같은 Bayes’ Rule을 이용하여 통계적 추론(statistical inference)을 수행한다. 눈여겨 볼 부분은, Frequentist와 달리 Bayesian은 보유한 사전적 정보를 prior distribution $Pr(\theta)$를 통해 통계적 추론에 반영한다는 것이다.
- $Pr(\theta)$ : prior probability - 사전적으로 $\theta$에 대해 가지고 있는 지식, 정보를 담은 분포
- $Pr(\mathbf{Z} \mid \theta)=L(\theta)$ : likelihood - parameter가 주어졌을 때, data의 조건부 density
- Frequentist가 사용하는 likelihood와 같은 의미.
- 지금의 관측된 data가 주어졌을 때, $\theta$의 각 값들이 얼마나 likely한가?를 의미.
- $Pr(\theta \mid \mathbf{Z})$ : posterior probability - data가 주어졌을 때, parameter의 조건부 density
- 기존에 가지고 있던 $\theta$에 관한 정보(prior)와 현재 관측된 정보(likelihood)를 합쳐, $\theta$에 대한 업데이트된 정보(Posterior)를 얻은 것.
즉, Bayesian의 통계적 추론은 “관측된 data를 보고 난 후, 업데이트된 $\theta$에 대한 우리의 지식”, 즉 Posterior distribution, $Pr(\theta \mid \mathbf{Z})$을 얻는 것이다. Posterior distribution을 얻었다면, 새로운 observation, $z^{new}$을 예측하는 predictive distribution, $Pr(z^{new} \mid \mathbf{Z})$을 얻을 수 있다.
\[Pr(z^{new} \mid \mathbf{Z})= \int Pr(z^{new} , \theta \mid \mathbf{Z}) d \theta= \int Pr(z^{new} \mid \theta , \mathbf{Z}) Pr(\theta \mid \mathbf{Z})d \theta\] \[Pr(z^{new} \mid \mathbf{Z})= \int Pr(z^{new} \mid \theta ) Pr(\theta \mid \mathbf{Z})d \theta\]마지막 식으로 넘어가는 과정에서 $Pr(z^{new} , \mid \theta , \mathbf{Z})=Pr(z^{new} , \mid \theta )$이 쓰였는데, 이는 각 observation이 $\theta$에 대해 conditionally independent하다는 것을 의미한다. 다만 이것이 frequentist들처럼 observation들이 서로 independent하다는 것을 의미하는 것은 아니다. 한 observation이 들어올 때마다 $\theta$에 대한 우리의 정보 및 주관적 믿음은 달라지기 때문에 observation이 서로 독립이 아니다. 하지만, $\theta$가 하나의 고정된 값으로 주어졌을 때의 조건부 분포의 상황에서는 observation들이 서로 독립이 되는 conditionally independent의 관계인 것이다.
새 observation, $z^{new}$에 대한 Predictive distribution, $Pr(z^{new} \mid \mathbf{Z})$은 $z^{new}$의 분포를 지금까지 관측된 것($\mathbf{Z}$)으로 얻은 posterior distribution, $Pr(\theta \mid \mathbf{Z})$로 기대값을 취한 형태이다. 다시 말해서 frequentist의 관점과 같이 $\theta$는 정해진 값이 아니라, $\theta$는 uncertain한 것이며, 가능한 $\theta$의 값들에 대한 우리의 현재의 지식, 믿음(Posterior)을 고려하여 새 observation $z^{new}$에 대한 예측을 하겠다는 것이다.
그와 반대로, Frequentist의 통계적 추론 방법인 maximum likelihood는 관측된 $\mathbf{Z}$로 보아 가장 Likely한 parameter 값, $\hat \theta_{MLE}$를 구하고, $Pr(z^{new} \mid \theta =\hat \theta_{MLE})$를 이용해 예측을 수행한다. 이는 위에서 언급한 Bayesian inference와는 다르게, $\theta$가 uncertain하다는 것을 반영하지 않은 접근이다.
8.4 Relationship Between the Bootstrap and Bayesian Inference
8.5 The EM Algorithm
한 문장으로 요약하자면, EM 알고리즘은 관측되지 않는 변수가 있을 때에도, 반복적인 알고리즘 수행을 통해 모수 추정을 가능하게 해주는 방법이다. 설명을 위해 아래와 같은 상황을 가정하겠다. 관심 확률변수벡터를 $\mathbf{T}=(\mathbf{Z},\mathbf{Z}^m)$이라고 하자.($\mathbf{Z}$와 $\mathbf{Z}^m$은 각각 여러 개의 확률변수를 포함하는 벡터이다.) 그 중 $\mathbf{Z}$는 관측이 된 데이터 $\mathbf{z}$가 있는 observable random variable이고, $\mathbf{Z}^m$은 관측되지 않는 Latent random variable이라고 하자. (ESL 교재 상의 notation인데 $\mathbf{Z}^m$의 $m$은 missing을 의미하는 것 같다.) 현재, 우리는 이 확률벡터 $\mathbf{T}$의 확률분포의 모수 $\theta$를 추정하고자 한다.
그러나, 지금 우리는 오도가도 못하는 상황에 처해있다. 모든 확률변수에 대해 관측된 data가 있다면, 그 data를 이용해 maximum likelihood와 같은 방법으로 모수 $\theta$를 추정하는 $\hat \theta$의 값을 얻을 수 있었을 것이다. 그러나 지금 우리의 관심 확률분포는 관측되지 않는 Latent random variable $\mathbf{Z}^m$을 포함하고 있다.
- 만약 모든 확률변수가 관측가능했더라면, $\theta$의 값을 추정하는 $\hat \theta$를 얻을 수 있었을 것.
- 그러나 $\mathbf{Z}^m$은 관측할 수 없는 Latent random variable. $\Longrightarrow \enspace \theta$의 값을 추정할 수 없다.
- 만약 $\theta$의 true 값을 알고 있었다면, 우리는 이 확률분포를 완전히 specify할 수 있게되고, 관측되지 않은 $\mathbf{Z}^m$의 분포도 알 수 있었을 것.
- 그러나 모수 $\theta$는 unknown constant. $\Longrightarrow \enspace \mathbf{Z}^m$의 분포 역시 알 수 없다.
즉, 정말로 간단하게 이야기하면 $\mathbf{Z}^m$을 모르니 $\theta$를 모르고, 또 반대로 $\theta$를 모르니 $\mathbf{Z}^m$를 모르는 상황인 것이다. 이 때, EM 알고리즘은 “만약 $\theta$를 안다면?”의 아이디어로 이 상황을 극복한다.
Algorithm
Initialize
EM 알고리즘은 모수의 값을 어떤 초기값으로 설정하는 것으로 시작한다. 이를 다음과 같이 나타내겠다.
\[\theta \leftarrow \theta^{(0)}\]Expectation step (E-step)
만약 우리의 모수, $\theta$의 값이 $\theta^{(0)}$이라는 것을 알고 있다면, 그리고 관측가능한 변수 $\mathbf{Z}$의 관측된 데이터 $\mathbf{z}$가 있다면, 우리는 이를 이용하여 관측할 수 없는 변수 $\mathbf{Z}^m$의 조건부 분포를 구할 수 있다.
\[P(\mathbf{Z}^m \mid \mathbf{Z}=\mathbf{z} \text{ , } \theta=\theta^{(0)})\text{ : conditional distribution of }\mathbf{Z}^m \text{given }\mathbf{Z}=\mathbf{z} \text{ , } \theta=\theta^{(0)}\]이를 간단하게 $P(\mathbf{Z}^m \mid \mathbf{Z}, \theta^{(0)})$로 나타내겠다. 이는 다음과 같은 예시로 생각해 볼 수 있다.
Jointly Normal 분포인 두 확률변수 $X,Y$가 있고, $Y$에 대한 데이터는 관측할 수 없는 상황을 가정해보자. Bivariate Normal 분포의 모수인 $\mu, \Sigma$의 초기값을 적당한 값 $\mu^{(0)}, \Sigma^{(0)}$로 설정하고, $P(Y \mid X, \mu^{(0)}, \Sigma^{(0)})$을 구한 것이다.
원래 관측불가능한 변수가 없는 경우였다면, 관측된 데이터를 이용해 Likelihood(혹은 log-likelihood)를 최대화하는 모수 $\theta$의 값을 찾았을 것이다. 그러나 우리는 ($\mathbf{Z}^m$이 빠진) 불완전한 데이터를 가지고 있기 때문에 Likelihood를 최대화할 수 없었다. 그래서 우리는 $\mathbf{Z}^m$의 조건부 분포를 이용해, log-likelihood에서 $\mathbf{Z}^m$을 marginalize 시키고자 한다. 이는 다음과 같은 방법으로 이루어진다.
\[Q(\theta \mid \theta^{(0)})=\mathbb{E}_{\mathbf{Z}^m \mid \mathbf{Z}=\mathbf{z} \text{ , } \theta=\theta^{(0)}} \Big[ \text{log-likelihood} \Big]= \sum_{\mathbf{Z}^m} \Big[ \text{log-likelihood} \Big]\cdot P(\mathbf{Z}^m \mid \mathbf{Z}=\mathbf{z} \text{ , } \theta=\theta^{(0)})\]이는 log-likelihood를 $\mathbf{Z}^m$에 대해 (조건부)평균을 취한 것이기 때문에, $\mathbf{Z}^m$의 가능한 값들에 대한 평균적인 log-likelihood를 구한 것이라고 이해할 수 있다. 관측이 되지 않아 $\mathbf{Z}^m$이 정확히 어떤 값을 갖는지는 모르지만, $\mathbf{Z}^m$이 가질 수 있는 값들에 대해서 평균적으로 log-likelihood는 어떤 양상일지를 구한 것이다. 따라서 이 $Q(\theta \mid \theta^{(0)})$를 “진짜 log-likelihood는 아니지만 그래도 평균적으로 log-likelihood가 어떤지를 나타내주는 함수이다”, “대리 log-likelihood function이다”라는 의미에서 Surrogate function이라고 부른다.
\[Q(\theta \mid \theta^{(0)})=\mathbb{E}_{\mathbf{Z}^m \mid \mathbf{Z}=\mathbf{z} \text{ , } \theta=\theta^{(0)}} \Big[ \log L(\theta \text{ ; } \mathbf{Z},\mathbf{Z}^m) \Big]\]Surrogate [ADJ] : a person or thing that is given a particular role because the person or thing that should have the role is not available.
Maximization step (M-step)
이제 우리는 $\mathbf{Z}^m$을 marginalize한, 즉 $\mathbf{Z}^m$를 포함하지 않는 대리 likelihood, $Q(\theta \mid \theta^{(0)})$를 가지고 있다. 이 $Q(\theta \mid \theta^{(0)})$를, 마치 이것이 우리의 likelihood인 것처럼, $\theta$에 대해 최대화하자. $Q(\theta \mid \theta^{(0)})$를 최대화하는 $\theta$를 구했다면, 그 $\theta$ 값을 우리의 새로운 $\theta$ 값으로 업데이트한다.
\[\theta^{(1)} \leftarrow \text{arg} \max_\theta Q(\theta \mid \theta^{(0)})\]Iterate
이제 이 새로운 $\theta$ 값인 $\theta^{(1)}$를 이용해, 다시 $\mathbf{Z}^m$의 조건부 분포를 구하고, log-likelihood에서 $\mathbf{Z}^m$을 marginalize하여 surrogate function을 얻은 뒤, surrogate function을 최대화하는 $\theta$를 구하는 이 전 과정을 반복한다. 그럼 우리는 업데이트되는 $\theta$ 값의 sequence를 다음과 같이 얻을 수 있다.
\[\theta^{(0)}, \theta^{(1)}, \theta^{(2)}, \theta^{(3)}, \cdots \enspace \rightarrow \enspace \theta^{\ast}\]위와 같이, 이 sequence가 어느 한 $\theta^{\ast}$로 수렴한다면, $\theta^{\ast}$는 EM algorithm을 통해 얻은 우리의 모수 추정치가 된다.
Application
EM 알고리즘은 위와 같이 관측불가능한 변수가 있는 상황에서, 모수를 추정해야하는 상황에 적용된다. 그 예시는 아래와 같다.
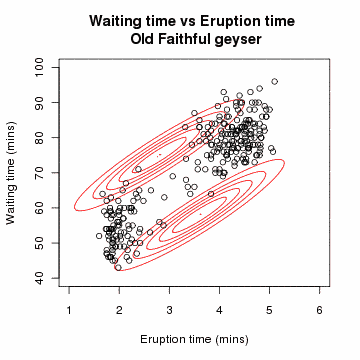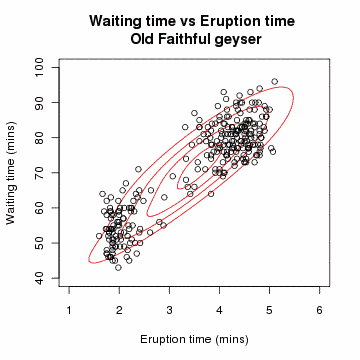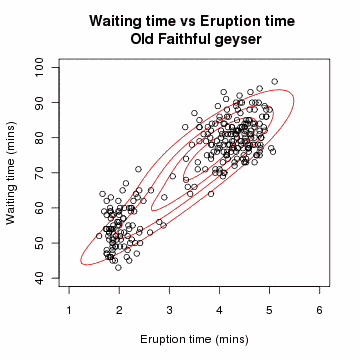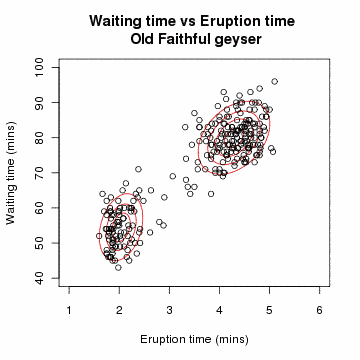
- Gaussian Mixture Model : 확률분포가 여러 Gaussian(Normal) 분포들의 mixture 형태로 이루어져 있다고 가정.
- 어떤 mixture component에서 생성된 data인지 나타내는 indicator variable을 latent variable로 두고 EM 알고리즘을 수행하여, 각 Gaussian 분포들의 모수인 mean vector와 covariance matrix를 추정.
- Gaussian Mixture Model을 정리한 포스트 Link

- Hierarchical Mixture of Experts(HME) model : 여러 Generalized Linear Model들을 계층적(hierarchical) mixture로 만든, Tree 구조의 supervised learning model.

Does It Really Work?
EM 알고리즘은 관측되지 않는 latent variable의 조건부 분포에 대해 likelihood를 marginalize(E-step)하고 그 결과인 surrogate function을 maximize(M-step)하는 작업을 반복한다. 이는 likelihood를 직접적으로 최대화하는 것이 아니다. 그렇다면 EM 알고리즘의 Iteration을 거칠 때마다 업데이트되는 $\theta$의 추정치가 likelihood를 개선시킨다는 것을 어떻게 정당화할 수 있을까? 이에 대한 설명은 아래 링크의 별도 포스트에 정리해두었다.
8.6 MCMC for Sampling from the Posterior
8.7 Bagging
8.8 Model Averaging and Stacking
8.9 Stochastic Search: Bumping
Reference
Hastie, T., Tibshirani, R.,, Friedman, J. (2001). The Elements of Statistical Learning. New York, NY, USA: Springer New York Inc..
