Contents
1. Introduction
2. Fitting Logistic Regression Model (binary response)
3. Fitting Logistic Regression Model (K-ary response)

1. Introduction

로지스틱 회귀분석은 반응변수 $G$가 $1$ 또는 $2$의 값을 갖는 Binary variable일 때, 혹은 $1,2,…,K$의 값을 갖는 $K$-ary variable일 때, 사용하는 회귀분석 모형이다. 이는 반응변수 $G$의 어떤 transformation이, $h(G)$, 예측변수 $X$에 대해 선형관계를 만족하는 일반화 선형모형(Generalized Linear Model)의 한 종류이다. 먼저 반응변수가 Binary variable일 때의 경우를 살펴보자. 로지스틱 회귀분석은 logistic 함수(혹은 sigmoid 함수)를 이용하여, $X$가 주어졌을 때 $Y$의 조건부 확률을 다음과 같이 가정한다.

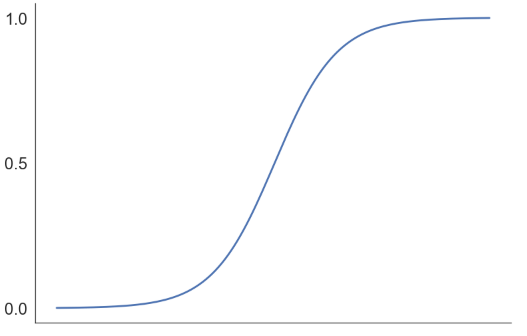
\[Pr(G=1|X=x)= \frac{e^{\beta^T x}}{1+e^{\beta^T x}} \enspace , \enspace \enspace Pr(G=2|X=x)=1- \frac{e^{\beta^T x}}{1+e^{\beta^T x}}=\frac{1}{1+e^{\beta^T x}}\]

위와 같은 형태로 $G$의 조건부확률을 가정한 이유는 확률은 $0\sim1$의 값을 가져야하고, logistic 함수($f(x)=\frac{e^x}{1+e^x}$)가 다음과 같이 $0\sim1$ 사이의 값을 갖기 때문이다.

우리는 예측변수 $X$가 변할 때, $G=1$과 $G=0$ 두 조건부확률의 차(difference)보다는 비(ratio)에 관심이 있다. 예를 들어, 어떤 도시에 비가 올 확률이 $0.6$이었다고 하자. 이 상황에서 비가 내릴 확률이 두 배가 되었다는 것은 단순히 그 확률에 2를 곱하여 비가 올 확률이 $1.2$가 된다는 것이 아니라, 날씨가 갤 확률 대비 비가 올 확률, 즉 확률비(ratio)가 $\frac{0.6}{1-0.6}=1.5$에서 $\frac{0.75}{1-0.75}=3$으로 두 배가 되었다는 것을 의미하기 때문이다. 이와 같은 두 조건부 확률의 비를 $odds$라고 한다. 로지스틱 회귀분석은 $log(odds)$를 다음과 같이 가정한다.

\[log\frac{Pr(G=1|X=x)}{Pr(G=2|X=x)}=log\frac{Pr(G=1|X=x)}{1-Pr(G=1|X=x)}=\beta^T x=\beta_0+\beta_1 x_1+...+\beta_p x_p\]

2. Fitting Logistic Regression Model (binary response)

그럼 데이터가 주어졌을 때, 이 로지스틱 회귀모형을 어떻게 fit할 것인가?

2.1. Likelihood Setting

$(x_1,g_1),(x_2,g_2),…,(x_N,g_N)$과 같이, random sample로 총 $N$개의 데이터를 가지고 있다고 하자.
$g_i$는 $1$ 또는 $2$의 값을 갖는 binary response variable이며, $x_i$는 각각 $p$개의 예측변수와, 상수항 계수에 대응될 $x_0=1$을 포함한 $p+1$차원 벡터이다. 따라서 추정할 회귀계수는 $\beta=[\beta_0,\beta_1,…,\beta_p]^T$가 된다. random sample $(x_1,g_1),…,(x_N,g_N)$에 대한 $\beta$의 likelihood는 다음과 같다.

\[L(\beta)=\prod_{i=1}^{N} P(G=g_i|X=x_i,\beta)\]

$g_i=1$일 때 $1$의 값을 갖고, $g_i=2$일 때 $0$의 값을 갖는 indicator function $y_i$를 도입하면 위 Likelihood 식은 아래와 같다.

\[L(\beta)=\prod_{i=1}^{N} P(G=1|X=x_i,\beta)^{y_i} P(G=2|X=x_i,\beta)^{1-y_i}\]

표현 상 편의를 위해, $P(G=1 \mid X=x_i,\beta)=p(x_i;\beta)=\frac{e^{\beta^T x_i}}{1+e^{\beta^T x_i}}$라고 하자.

\[logL(\beta)=l(\beta)=\sum_{i=1}^{N} \{ y_i logp(x_i;\beta) +(1-y_i)log(1-p(x_i;\beta)) \}\] \[= \sum_{i=1}^{N} \{ y_i log{e^{\beta^T x_i}} -y_i log(1+e^{\beta^T x_i})-(1-y_i)log(1+e^{\beta^T x_i}) \}= \sum_{i=1}^{N} \{ y_i \beta^T x_i -log(1+e^{\beta^T x_i}) \}\]

2.2. First-order Derivative

log-likelihood $l(\beta)$를 $\beta=[\beta_0,\beta_1,…,\beta_p]^T$에 대해 미분하자. i번째 observation의 에측변수를 담는 벡터 $x_i$는 아래와 같다.

\[x_i=[x_{i0},x_{i1},...,x_{ip}]^T=[1,x_{i1},...,x_{ip}]^T \enspace \enspace , \enspace i=1,2,...,N\]

이를 $\beta=[\beta_0,\beta_1,…,\beta_p]^T$의 $j+1$번째 원소 $\beta_j$에 대해 미분하면 다음과 같다.

\[\frac{\partial l(\beta)}{\partial \beta_j}=\sum_{i=1}^{N} \{ y_i x_{ij} -\frac{e^{\beta^T x_i}}{1+e^{\beta^T x_i}} x_{ij} \} \enspace \enspace , \enspace j=0,1,...,p\]

따라서 first-order derivative의 결과는 아래와 같다.

\[\frac{\partial l(\beta)}{\partial \beta}= \left[ {\begin{array}{c} \frac{\partial l(\beta)}{\partial \beta_0} \\ \frac{\partial l(\beta)}{\partial \beta_1} \\ \vdots \\ \frac{\partial l(\beta)}{\partial \beta_p} \\ \end{array} } \right] = \sum_{i=1}^{N} \{ y_i - p(x_i;\beta) \} \left[ {\begin{array}{c} 1 \\ x_{i1} \\ \vdots \\ x_{ip} \\ \end{array} } \right] = \sum_{i=1}^{N} \{ y_i - p(x_i;\beta) \} x_i\]

2.3. Second-order Derivative

log-likelihood $l(\beta)$를 $\beta_j$와 $\beta_k$로 미분하여 이계도함수를 구하면 다음과 같다.

\[\frac{\partial^2 l(\beta)}{\partial \beta_j \partial \beta_k} = \frac{\partial }{\partial \beta_k} \sum_{i=1}^{N} \{ y_i - p(x_i;\beta) \} x_i =- \sum_{i=1}^{N} x_{ij} \frac{\partial }{\partial \beta_k} p(x_i;\beta)\]

$p(x_i;\beta)=P(G=1 \mid X=x_i,\beta)=\frac{e^{\beta^T x_i}}{1+e^{\beta^T x_i}}$이므로,

\[\frac{\partial^2 l(\beta)}{\partial \beta_j \partial \beta_k} =- \sum_{i=1}^{N} x_{ij} x_{ik} p(x_i;\beta) (1-p(x_i;\beta))\]

log-likelihood를 $\beta=[\beta_0,\beta_1,…,\beta_p]^T$에 대해 두 번 미분하여 얻은 Hessian matrix의 $j$행 $k$열의 원소는 $\frac{\partial^2 l(\beta)}{\partial \beta_j \partial \beta_k} $ 이므로, Hessian matrix는 다음과 같다.

\[\frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} = \begin{bmatrix} \ddots & \vdots & \enspace \\ \cdots & \frac{\partial^2 l(\beta)}{\partial \beta_j \partial \beta_k} & \cdots \\ \enspace & \vdots & \ddots \\ \end{bmatrix} = - \sum_{i=1}^{N} p(x_i;\beta) (1-p(x_i;\beta)) x_i x_i^T\]

2.4. Newton-Raphson Method (Iteratively Reweighted Least Squares Method)

위와 같은 log-likelihood의 일계 미분 결과는 analytic하게 그 해를 찾을 수 없으므로, Newton-Raphson method를 이용하여 그 해를 찾을 것이다. Newton-Raphson method는 어떤 함수, $f(X)$, 의 값이 $0$이 되는 점을 찾는 데 쓰이는 대표적인 numerical method이다. Newton-Raphson method는 아래의 사진과 같이, 접선을 그려 그 접선함수의 값이 0이 되는 $X$값을 찾고, 새로 찾은 $X$ 값에서 다시 접선을 그리는 작업을 반복하여 함수의 값이 $0$이 되는 점을 찾는다.

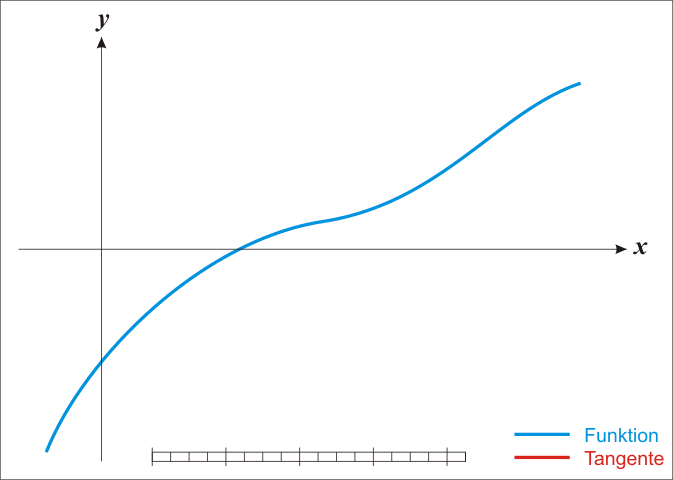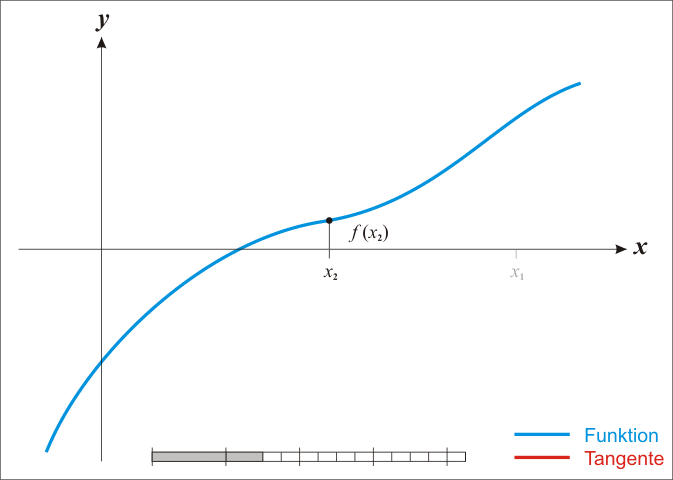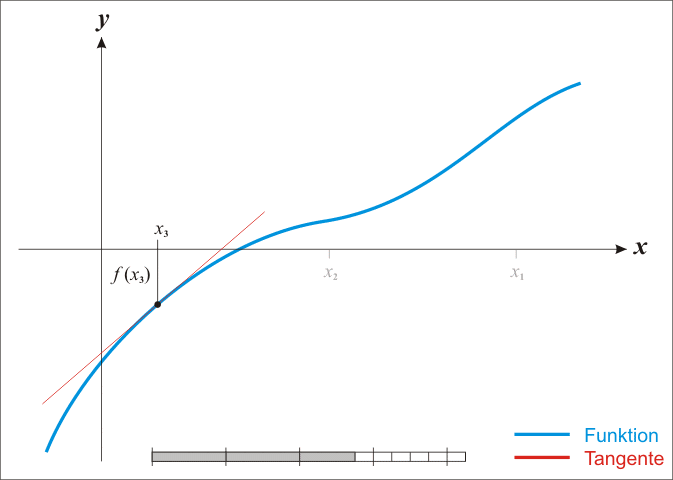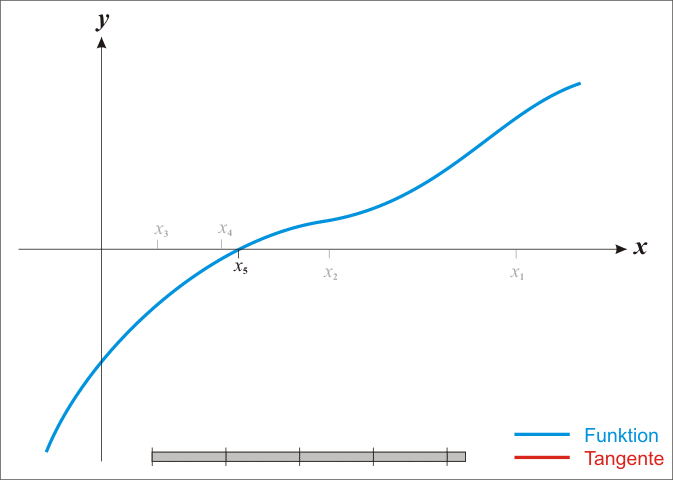
우리는 log-likelihood의 일계도함수 $\frac{\partial l(\beta)}{\partial \beta}$가 0이 되는 $\beta$를 찾고자 한다. 따라서 $\frac{\partial l(\beta)}{\partial \beta}$의 접선의 방정식과 같은 아래 식을 통해 $\beta$를 update시킨다.

\[0=\Big( \frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} \biggr\rvert_{\beta=\beta_{old}} \Big)(\beta_{new}-\beta_{old}) + \Big( \frac{\partial l(\beta)}{\partial \beta_j} \biggr\rvert_{\beta=\beta_{old}} \Big)\] \[\beta_{new}=\beta_{old} - {\Big( \frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} \biggr\rvert_{\beta=\beta_{old}} \Big)}^{-1} \Big( \frac{\partial l(\beta)}{\partial \beta_j} \biggr\rvert_{\beta=\beta_{old}} \Big)\]

위 식과 같이 $\beta$를 충분히 update시키면 $\frac{\partial l(\beta)}{\partial \beta}=0$을 만족하는 $\beta$를 numerical하게 찾을 수 있다.

이상의 결과를 행렬로 나타내면 보다 간단하게 나타낼 수 있다.

• $y$ : $N$개의 observed data의 각 $y_i$들로 만든 $N\times 1$ 벡터
• $X$ : $i$번째 observation의 예측변수벡터 $x_i$를 $i$번째 행으로 갖는 $N\times (p+1)$ 행렬
• $p$ : $N$개의 observed data에 대해, 각 $p(x_i;\beta)$들로 만든 $N\times 1$ 벡터
• $W$ : $p(x_i;\beta)(1-p(x_i;\beta))$를 $i$번째 diagonal element로 갖고, nondiagonal element는 모두 $0$인 $N\times N$ 정사각행렬

\[\frac{\partial l(\beta)}{\partial \beta}=X^T(y-p) \enspace \enspace , \enspace \frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} = -X^T WX\] \[\beta_{new}=\beta_{old} + (X^T WX)^{-1} X^T(y-p)= (X^T WX)^{-1} X^T WX \beta_{old} + (X^T WX)^{-1} X^T(y-p)\] \[= (X^T WX)^{-1} X^T W \Big( X \beta_{old} + W^{-1} (y-p) \Big)\] \[\beta_{new}= (X^T WX)^{-1} X^T W z\]

여기서 위와 같이 $z= X \beta_{old} + W^{-1} (y-p) $ 로 둔다면, Newton-Raphson method의 한 step 한 step이 지나며, $W$와 $z$ 역시 $\beta$의 값이 update 됨에 따라, 함께 update 될 것이다. Newton-Raphson method의 한 step으로 얻어진 $\beta_{new}$은 $z$를 response variable, $W$를 weight matrix로 두고 weighted least square를 수행한 결과와 같다고 볼 수 있다. 따라서 이와 같은 방법으로 로지스틱 회귀모형의 회귀계수 $\beta$를 추정하는 것을 Iteratively Reweighted Least Squares method이라고도 부른다.

3. Fitting Logistic Regression Model (K-ary response)

Reference

Hastie, T., Tibshirani, R.,, Friedman, J. (2001). The Elements of Statistical Learning. New York, NY, USA: Springer New York Inc..
Kutner, M. H., Nachtsheim, C., & Neter, J. (2008). Applied linear regression models. Boston: McGraw-Hill.